わけあって、線分\(XY\)と点\(Z\)が与えられた時に、点\(Z\)から線分\(XY\)へ下ろした垂線との交点\(M\)の座標を計算しました。結論からいうと、 \(\alpha = \frac{(X-Y)\cdot(Z-Y) }{||X-Y||^2}\) として、 \(M = \alpha X + (1-\alpha) Y\) になるようです。 \(\alpha\) は、点\(Z\)が \(X, Y\) のどちらに相対的に近いかを表していて、\(Z\) が\(X\)に近いほど1に近づき、\(Y\)に近いほどゼロに近づくことが式から分かります。 ほぼ１０年ぶりくらいにベクトル計算をしました。


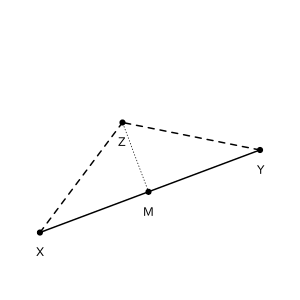
\(M\)は線分\(XY\)上にあるから、\(M = \alpha X + (1-\alpha) Y\)と書ける。 ベクトル\(MY\)と\(MZ\)が垂直であるので、その内積はゼロに等しい、つまり \begin{align*}
(M-Y) \cdot (M-Z) &= 0 \\
[ \alpha (X-Y) ] \cdot [ \alpha (X-Y) + (Y-Z)] &= 0 \end{align*}
ここで、 \( \cdot\) は内積を表す。これを解くと、 \begin{align*} \alpha^2 ||X-Y||^2 + \alpha (X-Y) \cdot (Y-Z) &= 0 \\ \alpha \left[ \alpha ||X-Y||^2 - (X-Y) \cdot (Z-Y) \right] &= 0 \end{align*}
ここで、 \(||\;\;||\) はユークリッドノルム。
\(\alpha=0\) は、\(MY\) がゼロベクトルになることで内積をゼロにするので、題意に合わない。よって \(\alpha = \frac{(X-Y)\cdot(Z-Y) }{||X-Y||^2}\).